今回は、三角形の内接円・外接円に関する公式をまとめました。
時間が足りなくなりがちな共通テストにおいて有効活用が期待できる公式なので、ぜひ利用できるようにしてください。
三角形の面積公式についてはこちら数学ⅠA:共通テストで使える便利な公式(三角形の面積編)
1. 内接円に関する公式
1-1. 内接円とは
内接円とは「ある多角形の内側に存在し、すべての辺に接する円」のことで、すべての多角形においてただ一つに定めることができます。
内接円の性質についてもっと知りたい方はこちら
1-2. 内接円に関する公式
〇内接円の半径と面積の関係式
△ABCの面積をSとすると
$S=\frac{1}{2}r(a+b+c)$

この関係式は主に、内接円の半径を求める際に使用します。
想定される問題の流れとしては、
- 余弦定理をもちいてある角の cos の値を求める。
- $\mathsf{sin}^2\theta+\mathsf{cos}^2\theta=1$ をもちいて cos を sin に変換し、面積を求める
- 面積と三辺の長さから上記の公式をもちいて内接円の半径を求める
三辺の値がシンプルな場合はヘロンの公式を利用して三角形の面積を求めることも検討してください。
ヘロンの公式についてはこちら数学ⅠA:共通テストで使える便利な公式(三角形の面積編)
2. 外接円に関する公式
2-1. 外接円とは
内接円とは「ある多角形の外側に存在し、すべての頂点を通る円」のことで、すべての多角形においてただ一つに定めることができます。
外接円の性質についてもっと知りたい方はこちら
2-2. 外接円に関する公式
正弦定理
〇正弦定理
外接円の半径をRとすると
$$\frac{a}{\mathsf{sin}A}=\frac{b}{\mathsf{sin}B}=\frac{c}{\mathsf{sin}C}=2R$$
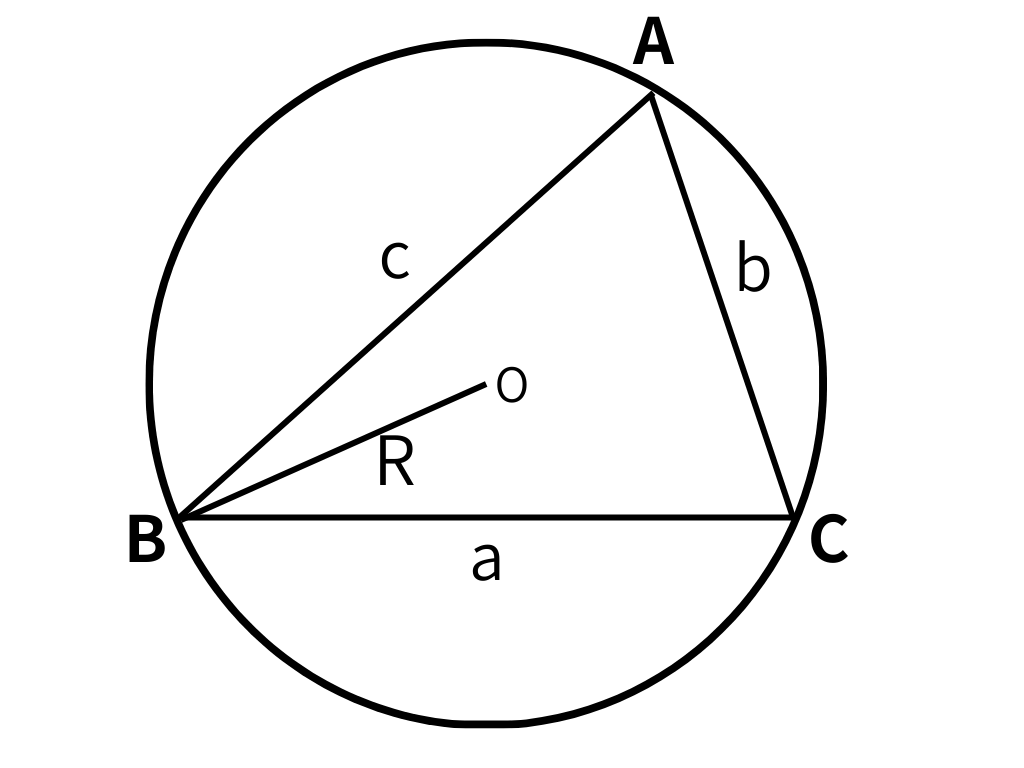
正弦定理をもちいることで、三角形の外接円の半径を求めることができます。
正弦定理は主に
- ある角と向かい合う1辺が与えられたとき
- 3辺が与えられたとき
に用いることができます。
想定される問題の流れとしては
- 向かい合う辺と角が与えられる
- 正弦定理をもちいて外接円の半径をもとめる
あるいは
- 3辺が与えられる
- 余弦定理をもちいてある角の cos の値を求める
- $\mathsf{sin}^2\theta+\mathsf{cos}^2\theta=1$ をもちいて cos を sin に変換する
- 正弦定理をもちいて外接円の半径を求める
などが考えられます。
外接円の半径と面積の関係式
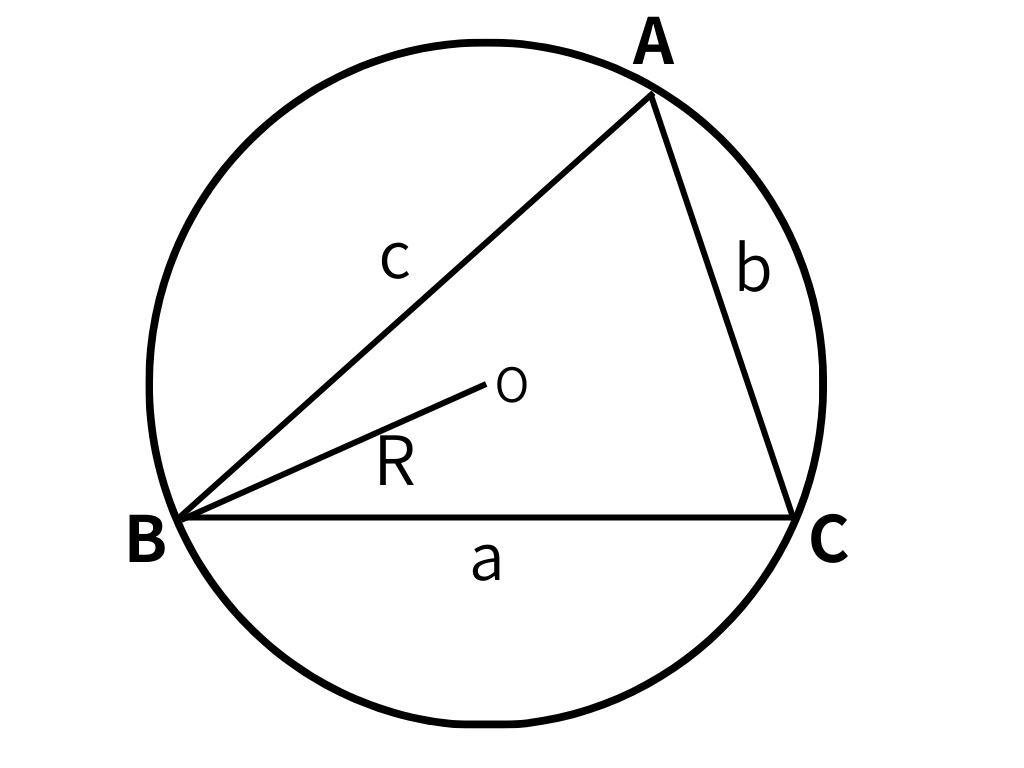
〇外接円の半径と面積の関係式
△ABCの面積をSとすると
$$S=\frac{abc}{4R}$$
この関係式は主に、外接円の半径を求める際に使用します。
三角形の面積の求め方は、先ほどと変わらず余弦定理やヘロンの公式をもちいて求めましょう。
まとめ
今回は、共通テストでの有効活用が期待できる内接円・外接円に関する公式を紹介しました。
検算や時短テクニックとしてぜひ活用してください。
数学の他のテクニックや他の科目の知識などをもっと学びたい方はこちら
ここまで読んでいただきありがとうございます。Study Hack Lab では、学び続けるみなさま、受験生のみなさまに向けて、勉強・習慣化・受験対策に関する有益な情報を提供しています。ぜひ他の記事もご覧ください。
📘科学的勉強法
効率よく学びたいあなたへ
エビデンスに基づいた学習理論を紹介します。
⏱習慣化の技術
習慣化に努めるあなたへ
「続ける仕組み」を脳科学・心理学的観点から紹介します。
🎯 受験戦略
受験生のあなたへ
受験に役立つテクニック、知識を筆者の経験を含めて共有します。

