今回は、三角形の面積公式を「与えられた条件別」にまとめました。
どの辺・どの角度が与えられているかで、面積を求めるアプローチを柔軟かつ素早く変更できるようになると、時間が足りなくなりがちな共通テストで点数を伸ばすことができるようになります。
ぜひ最後までご覧ください。
なお、各公式の証明は記事が長くなってしまうため、それぞれ別ページにて順次作成していきます。(2025/12/03)
1. $S=\frac{1}{2}ah$ :基本の公式
$S=\frac{1}{2}ah$
a:底辺 h:高さ
この公式は最も基本的な三角形の面積公式です。
主に座標平面状の三角形の面積を求めるときに用います。
だいたいの流れは以下の通りです。
- 座標が3点与えられる
- 点と直線の距離を公式をもちいて算出する(これが三角形の高さhにあたる)
- $S=\frac{1}{2}ah$ をもちいて面積を求める
〇点と直線の距離
点P($x_1$ , $y_1$)と直線 $ax+by+c=0$ の距離d
$$d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
2. $S=\frac{1}{2}bc\cdot\mathsf{sin}A$:三角比を含む公式
〇三角形の面積公式
$S=\frac{1}{2}bc\cdot\mathsf{sin}A$
$S=\frac{1}{2}ca\cdot\mathsf{sin}B$
$S=\frac{1}{2}ab\cdot\mathsf{sin}C$
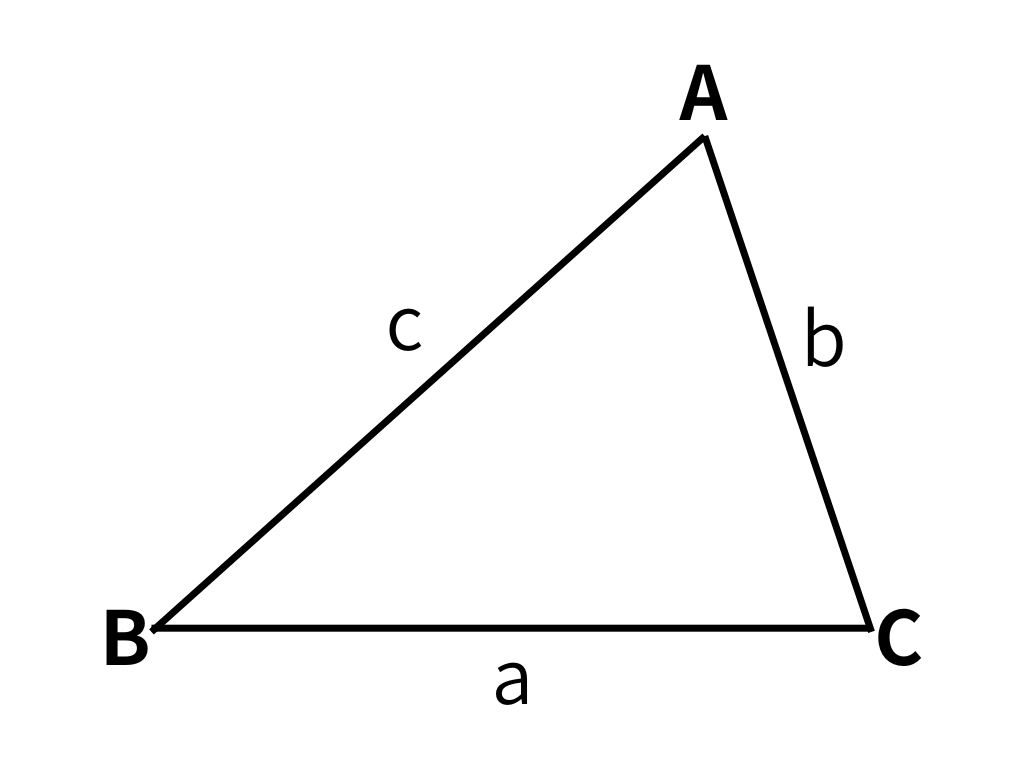
この面積公式は、「2辺とその間の角度」もしくは「3辺の長さ」が与えられたときに用いることができます。
今回は「3辺の長さ」が与えられたときの流れを解説していきます。
- 余弦定理を用いて任意の角の cos の値を求める
- $\mathsf{sin}^2\theta+\mathsf{cos}^2\theta=1$ より cos を sin に変換する
- 上記の面積公式を用いて面積を求める
〇余弦定理
$\mathsf{cos}A=\frac{b^2+c^2-a^2}{2bc}$
$\mathsf{cos}B=\frac{a^2+c^2-b^2}{2ac}$
$\mathsf{cos}C=\frac{a^2+b^2-c^2}{2ab}$
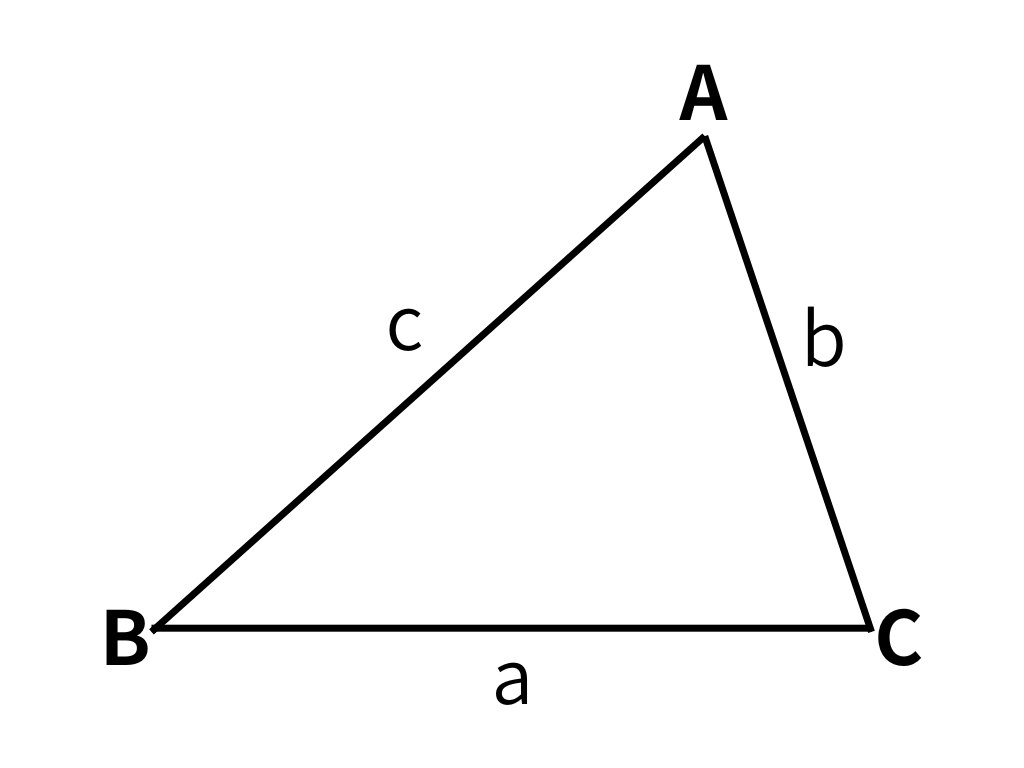
3. $S=\sqrt{s(s-a)(s-b)(s-c)}$:ヘロンの公式
〇ヘロンの公式
$$S=\sqrt{s(s-a)(s-b)(s-c)}$$
ただし
$$s=\frac{a+b+c}{2}$$

この公式は「3辺の長さ」が与えられていてかつ、「s の値がシンプルになる」ときに用いることができます。s の値が複雑になるときは1つ前のステップで紹介した方法を用いて面積を求めましょう。
まとめ
今回は三角形の面積を求める公式をまとめて紹介しました。「どのような条件が与えられているのか」から、適切なアプローチを選択して問題が解けるように演習を繰り返しましょう。
数学の他のテクニックや他の科目の知識をもっと体系的に学びたい人はこちら
ここまで読んでいただきありがとうございます。Study Hack Lab では、学び続けるみなさま、受験生のみなさまに向けて、勉強・習慣化・受験対策に関する有益な情報を提供しています。ぜひ他の記事もご覧ください。
📘科学的勉強法
効率よく学びたいあなたへ
エビデンスに基づいた学習理論を紹介します。
⏱習慣化の技術
習慣化に努めるあなたへ
「続ける仕組み」を脳科学・心理学的観点から紹介します。
🎯 受験戦略
受験生のあなたへ
受験に役立つテクニック、知識を筆者の経験を含めて共有します。

